
From the wave phase invariance ψ = ψ it would be naive to claim: Such a conclusion is incorrect because expression (3.4) depends on T both explicitly and implicitly. Let ψ be the phase of the radiation wave as measured in the inertial frame and let be the phase in the rotating frame.
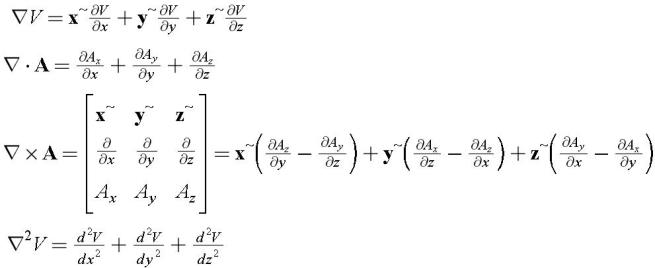
Source and let be the observed frequency. Let F obs be the frequency emitted by the radiation This is a critical issue in the explanation of the Mossbauer rotor experiments. Let’s Examine the Doppler Effect and electromagnetic beam aberration. (Where K = ( K x, K y, K z ) is the wave-vector of the electromagnetic front in frame (R, Φ, Z) Assume that in the inertial frame we have an electromagnetic wave propagating in the plane perpendicular to Z: ( E R, EΦ, E Z,) = ( A Sin (ωT- K.R),0, 0) ( B R, BΦ, B Z,)= (0,0, B Sin (ωT- K.Z) ) the same Rays as Viewed in an Inertial Frame. Substituting (2.9) in (2.7a),(2.7b) we get the general Maxwell equations in the rotating frame: Substituting (2.9) in (2.8a),(2.8b) we get the Maxwell equations in the rotating frame for the practical cases whereby the components of the vectors E, B do not depend of coordinates: ApplicationĪberration and Doppler Effect of Electromagnetic Rays Propagation in a Uniformly Rotating Frame vs. We know from the rules of vector transformation in cylindrical coordinates that: In practice, the components of the vectors E, B do not depend of coordinates, they may depend only on time, so the above equations simplify to: Equations (2.7a),(2.7b),(2.8a),(2.8b) mix variables from the inertial frame K and the rotating frame K’, we need to fix that.

The last two equations, written on a component by component basis, become:Ĭombining (2.5),(2.6) with (2.2) we get the Maxwell equations in the rotating frame: The above can be written, in cylindrical coordinates, according to (2.3) as: The Maxwell equations in the inertial frame are: The transformation between the frames is (Figure 1):įigure 1: Centrally rotating frame of reference The angular speed of rotation between the two frames is Ω. In a frame K ' rotating with respect the inertial frame, the coordinates are (t,r,ø, z). In an inertial frame K the coordinates are (Τ, R, Φ, Z). The euler-lagrange equations for motion on a uniformly rotating disc

In the present paper, we will construct a straightforward explanation by applying the formalisms developed in previous work. Usually, such experiments are explained from the perspective of an external, inertial frame because special relativity in rotating frames is viewed as more complicated. Our daily experiments happen in the laboratories attached to the rotating, continuously accelerating Earth. Real life applications include accelerating and rotating frames more often than the idealized case of inertial frames.


 0 kommentar(er)
0 kommentar(er)
